说明

时间限制：1 Sec 内存限制：256 MB 输入文件：box.in 输出文件：box.out

小明有 $n$ 块积木，高度都是 $1$，宽度均为 $2$ 的幂次，如 $1$、$2$、$4$、$8$、……。

小明的习惯不太好，玩过积木之后就摊在地上，妈妈为此非常头疼，所以她决定买个盒子。

已知盒子的宽度为 $W$（盒子一定能放得下最宽的一块积木）。不同的高度价格不同，所以妈妈希望买刚好能放进所有积木的盒子，不想花无谓的钱。

装积木时有个讲究，积木只能平放，例如，宽 $4$ 高 $1$ 的积木在盒子里只能占据横向为 $4$、纵向为 $1$ 的空间，而不能占据横向为 $1$、纵向为 $4$ 的空间。另外，积木也不能斜着放。

请帮妈妈计算一下至少要买高度为多少的盒子，才能装得下所有积木。

输入格式

第一行为一个整数 $t$，表示有 $t$ 组询问；

接下来为 $t$ 组输入，每组输入包含两行：

第一行为空格分隔的两个整数 $n$、$W$，表示有 $n$ 块积木、盒子的宽度为 $W$；

第二行为空格分隔的 $n$ 个整数 $w_1$、$w_2$、……、$w_n$。

输出格式

$t$ 行，第 $i$ 行为对第 $i$ 组询问的回答，为一个整数，表示至少要买高度为多少的盒子才能装得下所有积木。

样例

样例 1

2
5 16
1 2 8 4 8
6 10
2 8 8 2 2 8

2
3

样例说明：

在第 $1$ 组询问中，如下图所示为其中一种可行的放法，至少需要高度为 $2$ 的盒子。

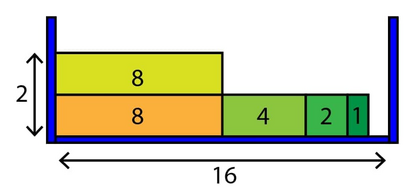
在第 $2$ 组询问中，可以在每一层都放一个宽度为 $2$ 和 $8$ 的木块，共放 $3$ 层。

数据范围

$1 \le t \le 10^4$

$1 \le n \le 2 \times 10^5$

$1 \le W \le 10^9$

$1 \le w_i \le 10^6$，$w_i$ 为 $2$ 的整数次方

在每一组询问中都有 $\max_{i=1}^{n}w_i \le W$

题目保证所有询问中的 $n$ 之和不超过 $2 \times 10^5$